tg-me.com/QMproblems/204
Last Update:
⭕️ مسئلۀ زمان؛ پاشنۀ آشیل نظریۀ کوانتوم
از ابتدای پیدایش نظریۀ کوانتوم بسیاری از فیزیکدانان بزرگ نسبت به آن ابراز ناخرسندی کرده اند. شرودینگر و اینشتین از اولین افرادی بودند که سعی داشتند با بیانی شفاف و منطقی، ناقص بودن این نظریه را اثبات کنند. (میتوانید پارادوکس گربۀ شرودینگر و پارادوکس EPR را ببینید). هربار که استدلالی بر علیه کوانتوم کپنهاگی ارائه میشد، بور و هایزنبرگ به نحوی از پاسخ طفره می رفتند و با زیر سوال بردن مفروضات اساسی علم، نظریۀ خود را تبرئه می کردند. موفقیت های تجربی این نظریه جامعۀ علمی را قانع کرده بود که معضلات آن را نادیده بگیرند و به حل مسائل دیگر در چارچوب این نظریه بپردازند. اما در این میان معضل بسیار عمیقی وجود داشت که خود را از چشم تیزبین بسیاری از فیزیکدانان با ذکاوت پنهان کرده بود.
اولین بار پائولی این معضل را با بور مطرح کرد. او که در مقام نظریه پردازی و آزمایش سرآمد بود، به مشکلی عمیق در نظریۀ کوانتوم پی برد. او گفت که ما در آزمایشگاه مکان و زمان برخورد ذرات به آشکار ساز را اندازه میگیریم. نظریۀ کپنهاگی مکان را به عنوان یک مشاهده پذیر به رسمیت میشناسد و برای آن یک عملگر در نظر میگیرد. اما در مورد زمان هیچ عملگر متناظری ارائه نمیدهد. در این نظریه، زمان صرفا پارامتری است که تحول تابع موج را توصیف میکند؛ ولی کوانتوم کپنهاگی هیچ پیشبینی ای دربارۀ زمان آشکارسازی ندارد. پائولی نشان داد اگر بخواهیم برای زمان یک عملگر تعریف کنیم باید طیف انرژی همواره پیوسته باشد (که میدانیم برای بسیاری از پدیده ها اینطور نیست) و همچنین حد پایینی برای انرژی سیستم نداریم (یعنی انرژی سیستم میتواند به منفی بینهایت میل کند).
بگذارید کمی واضح تر این مسئله را بیان کنم. تابع احتمال مکانی یک ذره به ما میگوید: اگر در یک زمان مشخص مکان ذره را اندازه بگیریم، در هر بازۀ مکانی چه مقدار احتمال دارد که ذره را پیدا کنیم. تصور کنید که ما در تمام نقاط فضا آشکارسازهای خاموشی را قرار داده ایم. در یک لحظه تصمیم میگیریم که همۀ آشکارسازها را روشن کنیم و تابع موج ذره را مجبور به کلپس (یا همان تقلیل)نماییم.این با چیزی که در آزمایشگاه اتفاق می افتد کاملا متفاوت است. ما در آزمایشگاه آشکارساز را در مکان مشخصی قرار میدهیم و منتظر میمانیم تا ذره خودش به آشکارساز برسد (و کلپس نماید)، و زمان رسیدن (یا کلپس) را اندازه میگیریم. اینکه چه قدر احتمال دارد که ذره را آشکار کنیم به مکان آشکارسازی و احتمال رسیدن ذره در آن زمان بستگی دارد. حال آنکه تابع احتمال مکانی صرفا یک تابع احتمال شرطی است. یعنی احتمال آشکارسازی ذره در فلان مکان به شرط اینکه کلپس در فلان زمان اتفاق بیافتد. ولی ما نمیدانیم در چه زمانی کلپس اتفاق می افتد!
شاید در نگاه اول مسئلۀ ساده ای به نظر برسد. ما احتمال مکانی ذره را در هر زمانی داریم. در نتیجه بدست آوردن احتمال زمان رسیدن ذره به یک مکان مشخص نباید خیلی سخت باشد. اما حقیقت این است که تابع احتمال شرطی مکان، نمیتواند اطلاعاتی دربارۀ تابع احتمال زمانی سیستم بدهد. این درحالی است که ما در آزمایشگاه همواره درحال اندازه گیری زمان هستیم. شاید برایتان جالب باشد؛ نظریۀ کوانتوم حتی در آزمایش دو شکاف معمولی هم نمیتواند احتمالات را به درستی برای ما پیشبینی کند. ما صرفا، با استفاده از تقریب های بسیار، طرح تداخلی را توجیه میکنیم. این موضوعی است که در کتاب های درسی به آن اشاره ای نمیکنند. اگر احیانا دانشجویی کنجکاو شود و برایش سوال پیش بیاید، اغلب توسط استاد درس به اصطلاح پیچانده میشود. البته اگر خوش شانس باشد و استاد به او القا نکند که «تو کم هوشی و این چه سوال بی ربطی است که میپرسی؟»
این موضوع به وضوح کامل نبودن نظریۀ کوانتوم و عدم توانایی آن در توضیح نتایج آزمایشگاهی را نشان میدهد. موضوعی که امثال اینشتین تلاش میکردند به صورت خیلی پیچیده تری آن را اثبات نمایند. نکتۀ جالب اینجاست که تا سال ۱۹۶۰ توجهی به این موضوع نشد تا اینکه آهارونوف و بوهم سعی کردند برای یک ذرۀ آزاد یک بعدی عملگری برای زمان آشکارسازی تعریف کنند. بعد از آن جریانی راه افتاد تا بتوانند به صورت اصول موضوعه ای تابع احتمال زمانی را استخراج نمایند. با وجود تلاش های بسیار تاکنون راه حل خالی از ایرادی برای این مسئله در چارچوب کوانتوم استاندارد ارائه نشده است و نظریات موجود تابع احتمال را صرفا برای ذرۀ آزاد یک بعدی بدست آورده اند. دیگر نظریات بدیل نیز توافق نظری با یکدیگر ندارند. اما در کوانتوم بوهمی، راحت تر میتوان به این مسئله پرداخت. چرا که در این نظریه ذرات مسیرهای مشخصی دارند که محاسبۀ زمان رسیدن آنها کار چندان دشواری نیست.
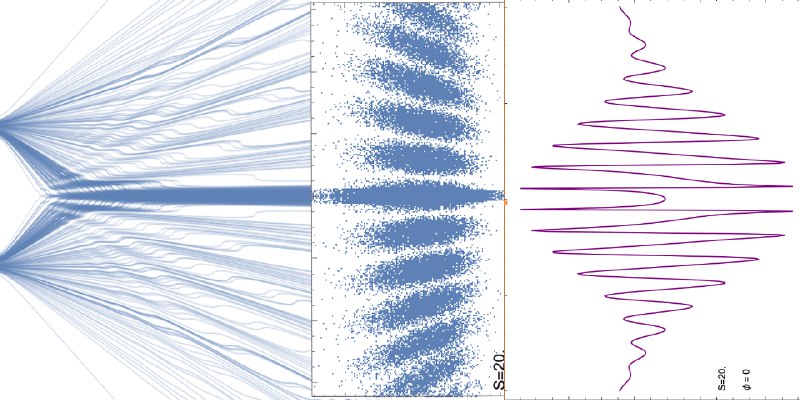
🔹 تصویر زیر مسیر ذرات، طرح تداخل زمانی و متوسط زمان رسیدن آنها در آزمایش دوشکاف است که در نظریۀ کوانتوم بوهمی شبیه سازی شده است
🆔@QMproblems
BY Quantum problems
Share with your friend now:
tg-me.com/QMproblems/204
